摘   要:为了研究RV减速器的振动特性，建立了RV-20E型RV减速器的刚柔耦合动力学虚拟样机模型，利用灰色关联度分析了样机的准确性。之后通过模态分析，分析了RV减速器的整机模态频率、振型等。进一步使用有限元方法对RV减速器进行了瞬态动力学分析，得到了不同工况下的仿真信号，并与试验测得的不同转速、负载下RV减速器的加速度振动信号进行对比，仿真分析结果与试验结果吻合度较高。分析结果表明负载对RV减速器振动的影响较小，而转速对于RV减速器的振动有明显影响。

关键词:振动特性;RV减速器;刚柔耦合动力学;模态分析

RV减速器由一级齿轮传动和一级摆线针轮传动组成，具有大传动比、传动效率高、结构紧凑等特点，是工业机器人的核心部件。在“中国制造2025”的概念下，机器人产业存在着巨大的发展空间，因此有必要推动RV减速器研究向更深层次发展。

早期对于RV减速器的研究重心主要放在传动精度、扭转刚度等^[1-3]方面，旨在解决RV减速器的基本制造问题。目前，对RV减速器的模态、振动等^[4]问题的研究也逐渐深入，以提高RV减速器在长期工作下的可靠性。RV减速器零件数量多、结构复杂，理论建模困难且存在诸多限制。一般基于理论推导的RV减速器的动力学模型往往需要诸多假设来简化模型^[5-7]，往往无法考虑零件变形、摩擦等非线性因素，且能够计算的内容有限，与实际工况存在差别。有限元方法一定程度上改善了理论建模的限制，已经在RV减速器的模态、摆线轮优化、受力分析等^[8-10]方面得以应用。基于刚柔耦合动力学^[11]的模型能够在考虑接触变形、啮合刚度等非线性因素的基础上，对减速器零部件的振动进行有效模拟^[12-15]，已经在机械工业中得到了有效运用。

本文以RV减速器为对象，首先对RV减速器整机进行了约束模态分析，得到了RV减速器的固有频率和振型。然后考虑齿轮啮合变形、齿面摩擦系数等因素，建立了RV减速器的刚柔耦合动力学模型。进一步应用了多体动力学相关知识，研究了RV减速器在不同载荷、不同转速工况下的加速度振动信号特征的变化。通过Workbench仿真与试验相结合的方式，分析了RV减速器加速度振动信号频谱的特点，以及转速、负载对RV减速器的影响，为后续进一步对RV减速器进行故障诊断、识别以及实时监测等研究提供依据。

1  RV减速器

RV减速器的传动简图如图1，主要包括小齿轮、行星齿轮、行星架、偏心轴、摆线轮、摆线针轮等部分。RV减速器的针轮与机架固定，通过小齿轮带动行星齿轮和偏心轴转动，偏心轴即围绕RV减速器的中心轴公转，又围绕自身中心轴自转，形成摆线运动。通过摆线轮与针轮的啮合，使得行星架转动。将行星架作为输出轴输出转速，实现传动力矩的作用。

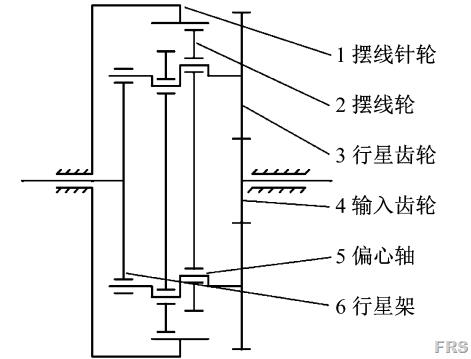
图1  RV减速器原理图

本文中建模、仿真所对应的RV减速器的摆线轮齿数为39，针轮齿数为40;小齿轮齿数12，行星齿轮齿数42。齿轮的压力角均为20°，模数均为1mm，偏心轴的偏心距1mm。

2  动力学分析

2.1模态分析

模态分析能够计算出模型的固有频率和振型，是研究机械振动特性的基础。一般系统的运动控制方程为

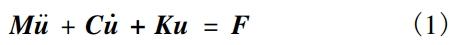
式中:u表示位移;M表示质量矩阵;C表示阻尼矩阵;K表示刚度矩阵。由于阻尼对系统的模态影响较小，故可以将阻尼项省略。无阻尼模态控制方程为

若所求为自由模态，即F=0，发生谐振时，求解公式

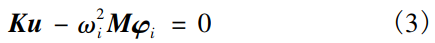
得特征值ω²_i与特征向量u，进一步计算即可得对应的模态频率和振型。

2.2刚柔耦合动力学

由于式(1)中的多个动力学方程相互耦合，无法单独求解，因此需要对动力学方程进行解耦。Craig-Bampton法^[16]是比较常用的方法，Craig-Bampton转换定义为

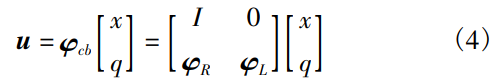
式中:φ_R为主模态矩阵;φ_L为约束模态矩阵;x为边界位移;q为模态坐标下的位移。式(4)中两边同时左乘φ^T_cb，变换后的质量、刚度矩阵以如下

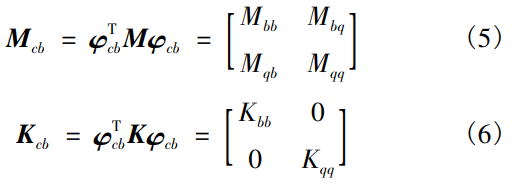
原方程组可以转换为

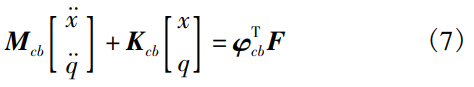
将φ^T_cb进行正则化后回代入原方程组，使得原方程组解耦。对解耦后的方程组进行计算求解，即可得到原耦合方程组的解。

3  虚拟样机建模与仿真

3.1建立模型

如图2所示。使用UG软件绘制RV减速器的三维装配体模型，Workbench软件中的Modal与Transient Structural模块进行刚柔耦合多体动力学分析。建模过程中，对模型进行了适当的简化，去除了对研究内容影响较小的倒角、圆角、螺纹等特征。考虑RV减速器实际工作过程中，行星架变形较小，其变形对整体的振动影响可忽略不计，因此将行星架设为刚体，不考虑变形;而齿轮间、摆线轮与针销之间存在摩擦、变形等非线性因素，对RV减速器的振动有明显影响，因此，需要将齿轮、摆线轮、针销等设置为柔性体，考虑变形因素引起的非线性。对于摩擦引起的非线性，考虑将小齿轮-行星齿轮接触面摩擦因数取0.1，摆线轮-针销的接触面之间的摩擦因数取0.08。由于偏心轴为RV减速器内部的重要受力部件，其刚度也相对于摆线轮等部件较低，因此需要考虑其变形影响，将其设置为柔性体。通过对小齿轮施加转速，行星架施加负载，模拟不同的实际工况。RV减速器中的轴承通过Workbench中的Bushing单元进行简化替代，行星架轴承、偏心轴轴承、偏心轴端部轴承根据有限元计算设置刚度为9.64×10⁸N·m、7.82×10⁸N·m、5.87×10⁸N·m。

模型通过Workbench中的自由网格划分方法划分四面体网格，对小齿轮-行星齿轮接触面和摆线轮-针销的接触面进行网格细化。模型最终包含147368个单元和317875个节点。该刚柔耦合模型相对于纯柔性体模型有效地减少了计算单元与节点的数量，增加了模型的计算速度。

图2  RV减速器模型

3.2模型验证

对于建立的RV减速器刚柔耦合动力学模型，需要进行一定的验证，以保证模型能够与理论结果比较吻合。灰色关联分析方法能够反应两个系统发展变化态势的相似程度，提供一个量化的度量，能够有效的用于模型的有效性检验。x与y的灰色关联系数的计算公式为

式中:ξ为分辨系数，一般在[0，1]之间选取，本文中选取分辨系数为0.5。关联度的计算公式为

当计算得到的关联度r大于0.5时，则可以认为两段数据的相关性较大。

本文采用恒定输入转速为200、400、600r/min的工况对虚拟样机进行灰色关联度分析。转速200r/min、负载60N·m时，输出转速如图3，转速曲线在开始有一定震荡，后续稳定在1.41r/min左右，有较小幅度的震荡。

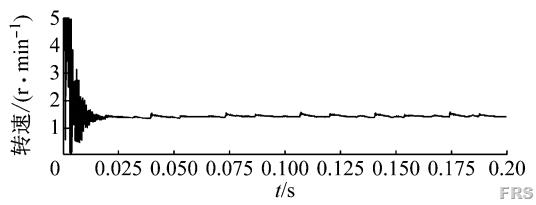
图3  RV减速器输出轴转速

选用的RV减速器理论传动比为141，理论输出转速分别为1.418、2.837、4.255r/min。从仿真中的行星架转速曲线中各抽取5个点，数据如表1，灰色关联度分别为0.800、0.822、0.887。可以认为建立的RV减速器模型能够应用到进一步的仿真当中。

表1  仿真输出转速

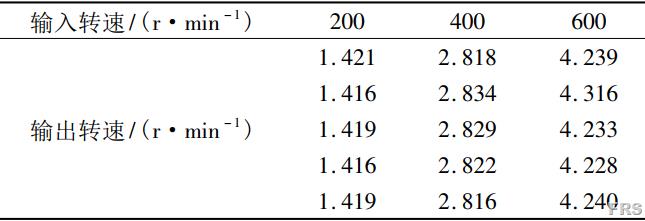
3.3整机模态分析

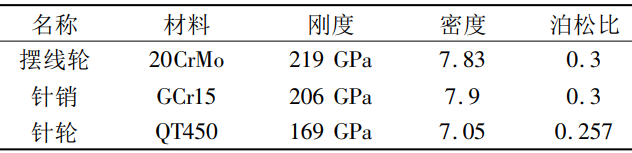
参考RV减速器加速度振动试验台的安装方式，对RV减速器进行整机约束模态分析。其中，主要的部件的材料系数设置如表2。

表2  不同零件材料参数

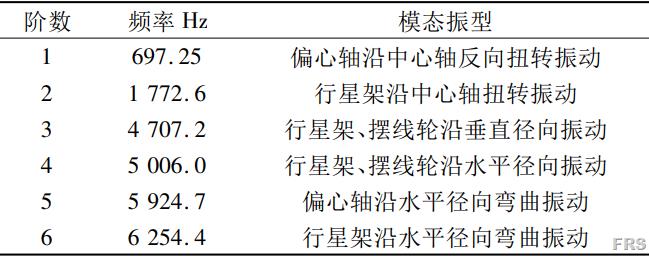
计算所得的固有频率与对应的模态振型如表3。

根据振型可知，RV减速器内部主要可能产生谐振的位置为齿轮、偏心轴与摆线轮。

表3  RV减速器前6阶模态频率

3.4动力学仿真

为了进一步了解RV减速器的振动特性，对RV减速器进行了不同转速、不同负载条件下的刚柔耦合多体动力学仿真，模型考虑了接触面摩擦因数、摆线轮变形、偏心轴弯曲等影响因素。本文中取仿真转速为200、400、600r/min，仿真时间为0.2s，仿真步长0.0002s。由于在仿真的初始条件为所有零件为静止状态，突变的转速会形成一个冲击，因此各个曲线在起始阶段变化较大，之后逐渐趋于稳定。文中截取稳定部分的仿真信号进行后续的数据分析。

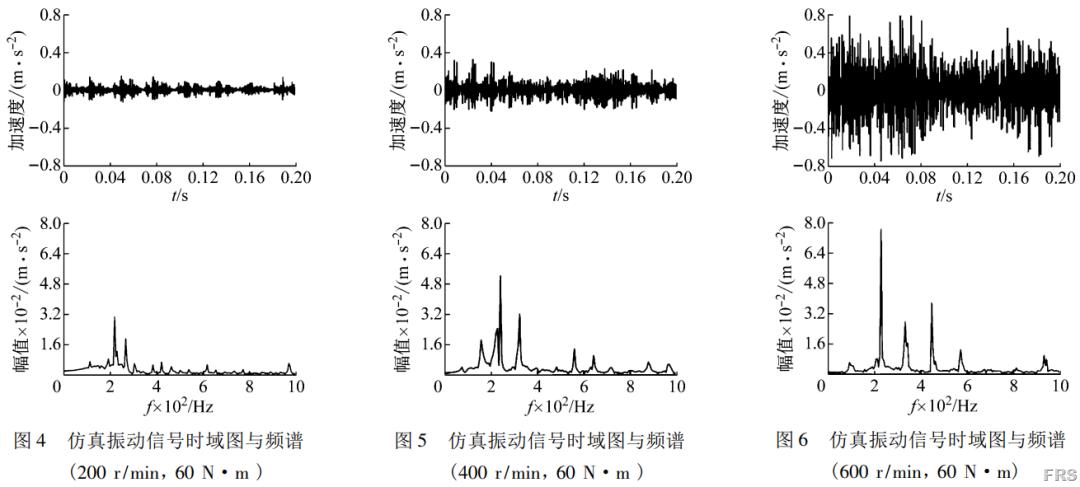
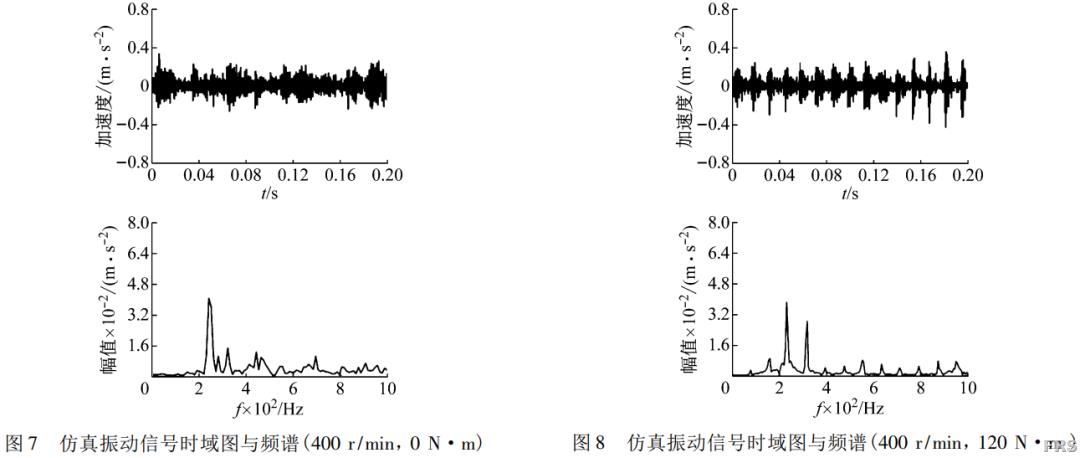
仿真模型中，选取节点编号为102898的网格节点进行RV减速器的振动加速度分析。由于篇幅有限，列出部分仿真结果，如图4～图8。图4～图6为转速不同，负载相同时节点102898垂直方向的加速度振动时域图与频域图。图5、7、8为转速相同，负载不同的情况下节点102898垂直方向的加速度振动时域图与频域图。

4  试验验证

4.1测试方法与设备

本文中采用的RV减速器加速度振动试验台如图9所示，通过电机通过联轴器与RV减速器的输入轴连接，带动减速器旋转。输出轴经过角度编码器、扭矩传感器后与磁粉制动器相连，构成一个功率开环系统。试验台中所用的各零部件型号如表4。

图9  RV减速器振动测试试验台

表4  试验台组件

4.2测点布置

试验中用于测试的传感器为电容式加速度传感器1C102，贴片式安装。传感器灵敏度20mV/(m/s²)，有效频率范围0～1000Hz，有效量程范围0～100m/s²。试验时，传感器通过胶水贴附于被测位置，采样频率2000Hz。考虑试验台与RV减速器的受力特点，本文主要采用被测位置水平径向和垂直径向两个方向的加速度振动信号。传感器布置位置如图10。

图10  传感器安装位置

4.3  RV减速器振动信号测试

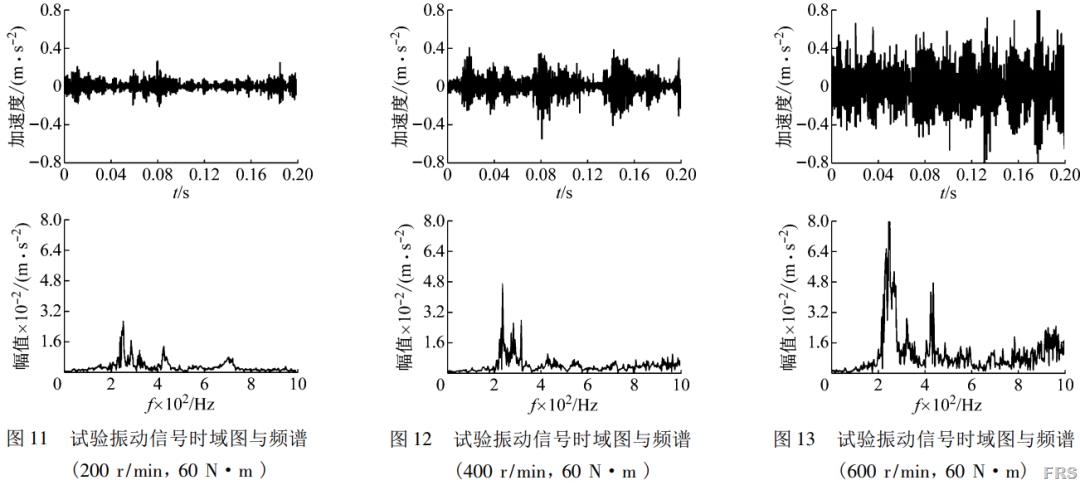
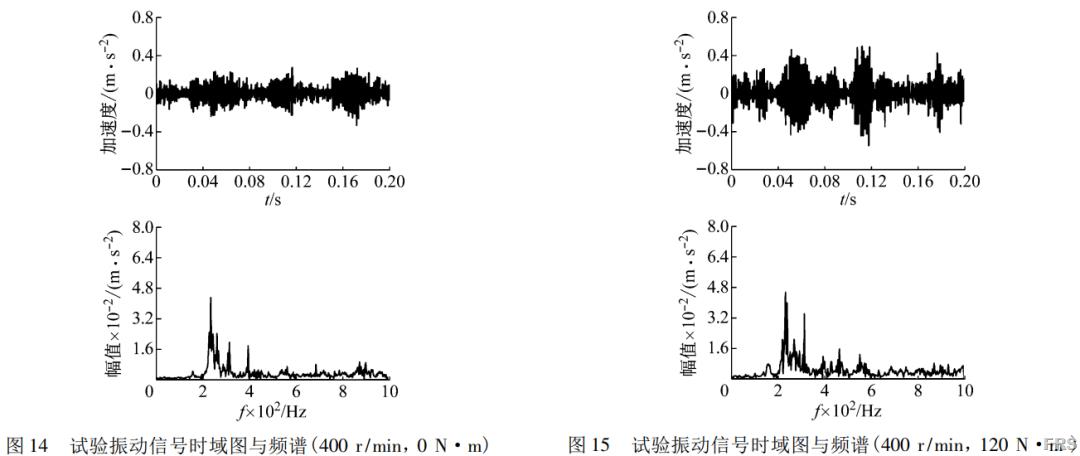
分别测试转速为200、300、400、500、600r/min，负载为0、30、60、90、120N·m时，RV减速器的加速度振动信号，每个工况分别独立测得3段数据，在后续的分析中，用平均值作为测试结果。最终测试所得到的部分数据如图11～图15所示。其中，图11～图13表示负载在60N·m，转速分别为200、400、600r/min时振动信号的时域图与频域图，反映转速对RV减速器振动的影响;同理，图12、14、15反映不同负载时振动的变化。

5  结果讨论

5.1特征值分析

不同转速负载下的RV减速器振动加速度仿真与试验值RMS值如表5。表5数据中，最大的RMS值相对误差为12.9%，此时的工况为转速200r/min，负载0N·m。RMS值随着转速、扭矩的增加而增加，而在RV减速器负载较高时，RMS值随着转速增加的速度变快。

表5  不同工况下的RMS值

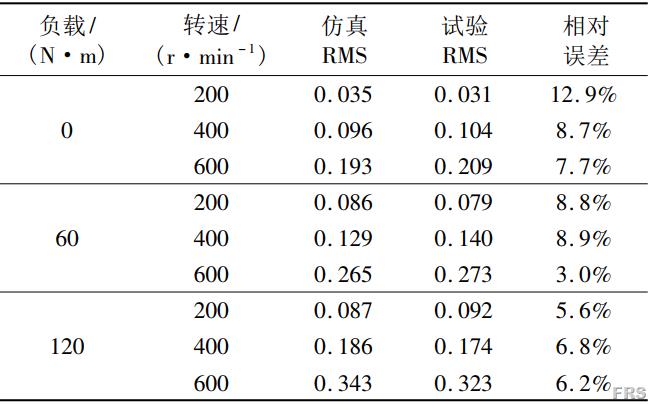
整体上，仿真信号的RMS值相对于与试验信号相差不大，RV减速器的刚柔耦合模型一定程度上能够正确反映RV减速器振动信号的有效值信息。

5.2频谱分析

由于仿真中采用的时间步为0.0002s，相当于5000Hz的采用频率，为了使其与试验采集信号相符合，对其进行降采样之后，通过FFT变换得到频谱图。从试验信号的频谱图11～图15中可以看出，试验测试的加速度信号中主要峰值频率在236.4、317.8、427.5Hz左右，与仿真信号的频率239.9、317.3、411.7Hz比较相近。此外，仿真信号频谱图整体的的峰值分布情况与试验值基本吻合。因此，认为RV减速器的刚柔耦合模型能够一定程度上正确反映出RV减速器振动信号的频谱特征信息。

5.3影响因素分析

(1)负载对RV减速器振动的影响

图12、14、15表明当RV减速器在不同的负载工况下工作时，特征频率与特征频率的分布变化较小，主要变化表现为320Hz附近的峰值大小随着负载的增加而增加，其它位置无明显变化。转速400r/min时，不同负载下320Hz附近峰值如图16。图中曲线表明，320Hz处峰值增长与负载大致成线性关系。

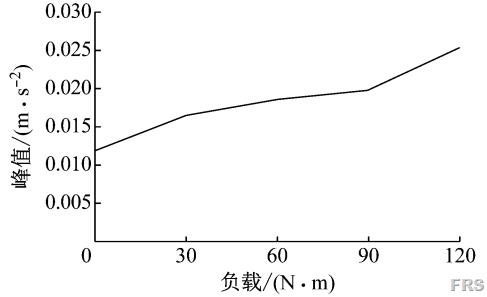
图16  转速400r/min不同负载下320Hz附近的峰值

图17为各个不同工况的测试信号的RMS值。可以看出在转速不变，负载增大时，信号的RMS值随之增大，增长近似于线性。

图17  不同转速与负载下的实验信号RMS

(2)转速对RV减速器振动的影响

对比图11、12、13，可以发现当转速变化时，节点加速度振动信号的频谱图发生了明显的改变，信号变化较大。200r/min的转速下，信号整体的加速度振动峰值较小，随着转速的增加，振动信号整体的峰值快速上升，且在频域中的分布也产生明显变化。结合图17，可以看出转速的改变对信号RMS值的影响要大于负载。

因此，可以判断转速会对RV减速器的振动产生相对于负载更加明显的影响。

6  结论

(1)建立了由摆线轮、摆线针轮、行星齿轮、偏心轴等零件组成的RV减速器整机刚柔耦合动力学模型。建模过程中考虑了偏心轴弯曲、中心轮-行星齿轮以及摆线轮-摆线针轮的接触、摩擦等非线性因素。进一步利用灰色关联分析法验证了模型。

(2)对RV减速器的整机约束模态进行了有限元仿真，计算得到了RV减速器整机的前六阶模态频率和模态振型。进一步通过瞬态动力学分析得到了RV减速器不同转速、转矩下的加速度振动信号。

(3)通过RV减速器加速度振动试验台对RV减速器的振动进行了测试。仿真信号与测试信号的分析表明RV减速器的振动受到负载、转速两方面影响，负载主要对振动信号的RMS有影响，对于RV减速器的频域分布影响较小;而转速对于两者均有较大的影响。仿真所得的振动信号与试验测试值在RMS、频谱上基本吻合，模型能够反映RV减速器实际工作时的信息。